[Zu den Übungsangaben] [Zum Java-Teil]
racket und die
Pakete, von denen es abhängt).
Die Vorteile von Racket für unsere Zwecke sind:
Nachdem Sie Racket installiert haben, können Sie drracket
starten, eine grafiktaugliche Umgebung für Racket. Allerdings müssen
Sie diese Umgebung erst noch einstellen, und zwar:
5und Racket gibt das Resultat "5" aus. Soweit, so uninteressant. Wir können den Computer auch rechnen lassen:
(+ 2 2) (* 12345 67890) (- 123 456) (/ 5 3) (- 5) (+ 1 2 3)Diese Notation nennt man Prefix-Notation, da der Operator vor den Operanden steht. Die konventionelle Notation (2+2) nennt man Infix-Notation.
Man kann auch verschachtelte Ausdrücke bauen
(+ 7 (* (+ 5 3) (- 5 3)))Da jeder Unterausdruck explizit geklammert ist, braucht man keine Präzedenzregeln ("Punktrechnung vor Strichrechnung").
Die Auswertung erfolgt, indem zuerst die inneren Klammern berechnet werden, und dann die nächstinneren, bis schließlich der komplette Ausdruck berechnet ist:
(+ 7 (* (+ 5 3) (- 5 3))) (+ 7 (* 8 2)) (+ 7 16) 23Sie können sich das mit dem Debug-Modus von DrRacket anschauen (dazu den Ausdruck in den oberen Bereich schreiben).
Sie können das Quadrat von verschiedenen Zahlen wie folgt berechnen:
(* 5 5) (* 27356 27356)aber dabei müssen wir die Zahl immer zweimal eingeben, was mühsam und fehleranfällig ist. Sie können aber auch eine Funktion dafür schreiben:
(define (qu x) (* x x))In DrRacket geben Sie diese Funktion am besten oben ein, dann überlebt sie das nächste Strg-T.
Jetzt können Sie verschiedene Quadrate berechnen, indem Sie die
Funktion qu mit dem passenden Parameter aufrufen:
(qu 5) (qu 27356)(Funktions-)Parameter bezeichnet einen veränderlichen Wert einer Funktion, der an die Funktion explizit übergeben wird. Dabei unterscheidet man zwischen dem formalen Parameter (hier
x) und dem tatsächlichen Parameter (hier 5
bzw. 27356). Oft wird stattdessen auch der Begriff Argument
verwendet, vor allem für den tatsächlichen Parameter.
Was passiert hier bei der Auswertung von (qu 5)? Der
Ausdruck (* x x) wird ausgewertet, wobei 5
an xgebunden ist, die Auswertung von x also
den Wert 5 ergibt.
Sie können diese Funktion jetzt so verwenden wie die eingebauten auch, also auch in anderen Funktionen:
(define (kreisflaeche r) (* 3.14 (qu r)) (kreisflaeche 10) (define (hoch4 y) (qu (qu y))) (hoch4 3)Beim letzten Beispiel ist interessant, dass
qu
verschachtelt aufgerufen wird. Was passiert da mit x.
Allerdings wird hier zuerst (qu 3) aufgerufen, und erst
wenn das fertig ist, (qu 9), sodass sich hier die Frage
noch nicht so dringend stellt. Interessanter wird es, wenn
wir hoch4 so definieren:
(define (hoch4 x) (qu (qu x)))Dieses Programm liefert das gleiche Ergebnis wie das obige: Bei der Auswertung von
(hoch4 3) wird 3 an das x von
hoch4 gebunden, dann beim Aufruf von (qu 3) 3 an
das x von qu und dann 9 an
das x von qu. Jede Funktion hat also ein
eigenes x; tatsächlich hat jeder Funktionsaufruf
sein eigenes x, wie wir später sehen werden.
Man kann diese Bindungen bei der Auswertung von Funktionen in Racket auch explizit darstellen:
(hoch4 3) (let ((x 3)) (qu (qu x))) (let ((x 3)) (qu (let ((x 3)) (* x x)))) (let ((x 3)) (qu (let ((x 3)) (* 3 3)))) (let ((x 3)) (qu (let ((x 3)) 9))) (let ((x 3)) (qu 9)) (let ((x 3)) (let ((x 9)) (* x x))) (let ((x 3)) (let ((x 9)) (* 9 9))) (let ((x 3)) (let ((x 9)) 81)) (let ((x 3)) 81) 81Wichtig ist dabei, dass jeder Aufruf von
hoch4
und qu ein neues Exemplar von x in's Spiel
bringt.
Im Englischen werden solche Exemplare als instances bezeichnet, daher nennen Informatiker Exemplare auch oft Instanzen.
x in den let-Ausdrücken ist ein Beispiel
für eine Variable in der Informatik. Dieser Begriff hat eine
andere Bedeutung als in der Mathematik und bezeichnet einen Namen, an
den ein Wert gebunden ist, wobei im Normalfall verschiedene Exemplare
der Variable verschiedene Werte bekommen, und sich in den meisten
Programmiersprachen der Wert eines Exemplars im Laufe der Zeit ändern
kann. Parameter sind auch Variablen.
(< 5 3) (= 3 3)Wozu kann man das gebrauchen? Um bedingte Ausdruecke zu schreiben:
(if (< (* 37 33) 1200) 5 10)Das
if wertet zuerst den ersten Ausdruck aus; ist das
Ergebnis #f, dann wird der dritte Ausdruck ausgewertet
und sein Ergebnis ist das Ergebnis der if-Ausdrucks,
sonst der zweite. Also:
(if #t 2 3) (if #f 2 3) (if 1 2 2)Solche bedingten Ausdrücke setzt man sinnvollerweise in Funktionen ein, weil die Entscheidung dort von den Parametern abhängt und bei verschiedenen Aufrufen der Funktion verschieden ausfallen kann.
(define (max a b) (if (> a b) a b)) (max 3 5) (max -3 -5)
(define (hoch x n) (if (= n 0) 1 (* x (hoch x (- n 1))))) (hoch 3 0) (hoch 3 4) (hoch 3 0.5)Der dritte Ausdruck leitet sich aus der mathematischen Äquivalenz
x*xn = xn+1
bzw.
xn = x * xn-1
ab, der zweite aus
x0 = 1
Wie funktioniert aber die gesamte Funktion?
(hoch 3 2) (let ((x 3)(n 2)) (if (= n 0) 1 (* x (hoch x (- n 1))))) (let ((x 3)(n 2)) (* x (hoch x (- n 1)))) (let ((x 3)(n 2)) (* x (let ((x 3)(n 1)) (if (= n 0) 1 (* x (hoch x (- n 1))))))) (let ((x 3)(n 2)) (* x (let ((x 3)(n 1)) (* x (hoch x (- n 1)))))) (let ((x 3)(n 2)) (* x (let ((x 3)(n 1)) (* x (let ((x 3)(n 0)) (if (= n 0) 1 (* x (hoch x (- n 1))))))))) (let ((x 3)(n 2)) (* x (let ((x 3)(n 1)) (* x (let ((x 3)(n 0)) 1))))) (let ((x 3)(n 2)) (* x (let ((x 3)(n 1)) (* x 1)))) (let ((x 3)(n 2)) (* x (let ((x 3)(n 1)) 3))) (let ((x 3)(n 2)) (* x 3)) (let ((x 3)(n 2)) 9) 9In einer rekursiven Funktion muss es (mindestens) eine Abbruchbedingung geben, die dazu führt, dass die Funktion nicht noch einmal aufgerufen wird, hier
(= n 0). Und beim
rekursiven Aufruf müssen der Parameter, der in der Abbruchbedingung
vorkommt, sich so ändern, dass die Abbruchbedingung irgendwann einmal
zutrifft.
In unserem Beispiel ist das allerdings nur für ganzzahlige positive n
der Fall. Mehr war zwar auch nicht verlangt, aber eine
Endlosrekursion bei falscher Eingabe ist meist eine suboptimale
Lösung.
Ein weiteres Beispiel für Rekursion ist
die Fibonacci-Folge,
definiert als:
f0 = 0
f1 = 1
fn = fn-1+fn-2
In Racket direkt ausdrückbar wie folgt:
(define (fib n) (if (< n 2) n (+ (fib (- n 1)) (fib (- n 2))))) (fib 5) (fib 10) (fib 40)Diese Definition ist zwar nahe an der mathematischen Definition, aber ineffizient, weil die gleichen Funktionswerte mehrmals bis extrem oft berechnet werden: Hier eine graphische Darstellung:

Exkurs: Dieser Graph (aus der mathematischen Graphentheorie), in der jeder Knoten mit jedem anderen über genau einen Weg verbunden ist, wird Baum genannt, und ist in der Informatik eine sehr häufige Struktur. In der Informatik hat man es fast immer mit gerichteten Bäumen zu tun, bei denen ein Knoten als Wurzelknoten bezeichnet wird, zu dem keine Kante führt; zu jedem anderen Knoten führt genau eine Kante. Knoten, von denen keine Kanten wegführen, heissen Blätter, die anderen heissen interne Knoten. Wenn, wie hier, von einem internen Knoten jeweils zwei Kanten weggehen, spricht man von einem binären Baum. Gerichtete Bäume werden meist so dargestellt, dass die Kanten von oben nach unten führen (die Wurzel also oben ist, im Gegensatz zu natürlichen Bäumen), und daher spart man sich meistens die Darstellung der gerichteten Kanten als Pfeile.
Dieser Graph stellt unsere Aufrufe dar und wird daher als Aufrufbaum bezeichnet.
Schon bei der Auswertung von (fib 5) wird fib insgesamt 15 mal aufgerufen, darunter 5 mal (fib 1). Der Grund liegt in den zwei rekursiven Aufrufen in fib. Insgesamt zeigt diese Version von fib eine Laufzeit, die exponentiell von n abhängt.
Eine effizientere Art der Berechnung lässt sich daraus ableiten, wie man die Folge händisch berechnet: f0 und f1, sind gegeben, daraus berechnet man f2, dann f3, usw., bis man bei dem gesuchten fn ist. Dabei benötigt man bei der Berechnung immer die beiden vorhergehenden Elemente der Folge.
Wir können diese Berechnung als rekursive Funktion ausdrücken:
(define (fib n)
(f n 0 0 1))
(define (f n i fi fi1)
(if (= i n)
fi
(f n (+ i 1) fi1 (+ fi fi1))))
Dabei führt jeder Aufruf von f einen Schritt der Berechnung durch.
Die Parameter haben folgenden Zweck: n gibt das Ziel-Element der Folge
vor (wir wollen fn berechnen), i ist der Index des aktuell
berechnete Elements (also von fi). fi ist der Wert von
fi, und fi1 ist der Wert von fi+1.
Die Aufrufe von f beginnen mit i=0, fi=0, fi1=1 (in der Definition von fib). Wenn n schon erreicht wurde, ist fi das Resultat, und rufen f erneut auf, mit i+1 als zweitem Argument (formaler Parameter i), fi+1 für fi, und das neu berechnete fi+2 für fi1.
Ein Aufrufbaum unserer neuen Formulierung schaut wie folgt aus:
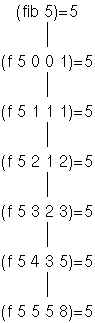
Ein Unterschied zur ursprünglichen Formulierung, bei der die Zwischenergebnisse als Funktionsresultate zurückgegeben werden, ist, dass hier die Zwischenergebnisse als Parameter weitergegeben werden und nur das Endergebnis als Funktionsresultat zurückgegeben wird.
Bei der ursprünglichen Formulierung und bei hoch steht
jeder Aufruf für sich selbst, hier ist f eigentlich nur eine
Hilfsfunktion fuer fib und ergibt für sich alleine wenig Sinn.
Allerdings hängt diese Art der Forumlierung nicht mit dem exponentiellen Rechenaufwand zusammen: Man kann auch eine exponentielle Definition von fib erstellen, wo die Zwischenergebnisse als Parameter weitergereicht werden, und (mit Sprachkonstrukten, die noch nicht vorgestellt wurden) eine mit linearem Aufwand, in der die Zwischenergebnisse zurückgegeben werden.
Die andere wichtige Eigenschaft ist, dass am Schluss das richtige
Ergebnis herauskommt. Dazu ist es hilfreich, wenn schon die
Zwischenergebnisse in irgendeiner Hinsicht richtig sind. Dazu
beschreibt man die Zwischenergebnisse mit Invarianten, das sind
Gleichungen (manchmal auch Ungleichungen), die für alle
Zwischenergebnisse zutreffen. Für die Hilfsfunktion f
bei der Fibonacci-Funktion kann man z.B. folgende Invarianten
formulieren:
fi = fi fi1 = fi+1wobei mit fx auf das x-te Element der Fibonaccifolge gemeint ist und mit i der Parameter i des gleichen Aufrufs.
Wenn i=n, hat man in fi den gesuchten Wert fn.
Für diese Invarianten müssen alle Aufrufe von f die Invarianten erfüllen. Der Aufruf in fib erfüllt die Invarianten (trivial zu überprüfen), und der Aufruf in f erfüllt sie auch (da muss man vielleicht etwas länger überlegen).
Wie kommt man auf diese Invarianten? In diesem Fall kann man sie aus der Grundidee für diese Formulierung von fib ableiten. Der Vorteil von Invarianten gegenüber der Grundidee ist, dass es nur ein Teilaspekt ist; bei komplizierteren Fällen ist es einfacher, über die Aspekte einzeln nachzudenken und sie zu überprüfen als die ganze komplizierte Idee auf einmal zu betrachten.
Da ein Programm normalerweise abhängig von Parametern bzw. Eingaben viele verschiedene Abläufe zur Laufzeit haben kann, ist es zum Verständnis des Programms sinnvoll, wenn man von diesen verschiedenen Abläufen abstrahieren kann, indem man gemeinsame Eigenschaften beschreibt. Bzw. umgekehrt, wenn man das Programm so schreibt, dass man mit einer statischen Beschreibung wichtige Eigenschaften beschreiben kann. Invarianten sind so eine statische Beschreibung.
Als weiteres Beispiel kann man neben dem dynamischen Aufrufbaum unserer zweiten Definition von fib auch einen statischen Aufrufgraphen zeichnen:
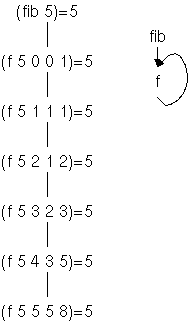
Beim statischen Graphen habe ich die Parameter und Resultate weggelassen, da die konkreten Werte nicht bekannt sind. Der rekursive Aufruf von f wird im Aufrufgraphen als Zyklus dargestellt. Da der Graph kein Baum ist, wird die Richtung der Kanten durch Pfeile dargestellt.
Unter den Programmiersprachen gibt es auch statischere und
dynamischere. Zum Beipiel ist Java statischer als Racket: In Java
muss man für jede Variable statisch einen Typ (z.B. int)
hinschreiben, und es wird während der Compilation überprüft, ob die
Typen mit den Operationen zusammenpassen, und ggf. meldet der Compiler
einen Fehler. In Racket schreibt man dagegen die Variablen ohne Typ,
und man kann verschiedene Typen als Parameter übergeben; erst die
Operationen überprüfen zur Laufzeit, ob der Typ passt, und Typfehler
werden daher erst zur Laufzeit gemeldet.
(define (inc x) (+ x 1)) (inc 1) ;inc funktioniert mit ganzen Zahlen (inc 1.0) ;inc funktioniert mit reals (inc "a") ;inc funktioniert nicht mit Zeichenketten (strings)Was besser ist und warum, wurde schon oft und lange diskutiert; sowohl statisch typisierte (Java, C++, C) als auch dynamisch typisierte Programmiersprachen (Python, Ruby, PHP) werden häufig verwendet, und es sieht nicht so aus, als ob sich eine Klasse gegenüber der anderen in allen Gebieten durchsetzen würde.
Aber auch bei Verwendung von dynamischen Programmiersprachen wird man das Programm verstehen, indem man über verschiedene Abläufe statisch abstrahiert. Im Beispiel mit dem Typ des Parameters von inc wir man sich überlegen, dass inc nur auf Zahlentypen funktioniert, und wird inc daher nur mit Zahlen als Parameter aufrufen; das sind beides statische Eigenschaften.
Der Vorteil der dynamischen Sprache hier ist, dass man frei ist, sich beliebige statische Abstraktionen zu überlegen, während man sich bei der statischen Sprache auf die von der Programmiersprache vorgegebenen Konzepte einschränken muss.
Dafür ist der Vorteil der statischen Sprache, dass eine Reihe von Fehlern schon vom Compiler erkannt werden, während diese Fehler bei dynamischen Sprachen erst beim Testen erkannt werden (und dazu muss man die Tests auch so vollständig machen, dass sie den Fehler aufdecken, aber das sollte man ohnehin machen).
(define (fib n)
(define (f n i fi fi1)
(if (= i n)
fi
(f n (+ i 1) fi1 (+ fi fi1))))
(f n 0 0 1))
Man kann die Funktion g nicht von aussen aufrufen, und wenn man aussen
eine Funktion g definiert, beeinflusst das fib nicht:
(f 5 0 0 1) (define (f w x y z) -1) (fib 5)Wie bei den Variablen wird beim Aufruf die jeweils nächste umgebende Funktion des Namens verwendet, im Beispiel bezieht sich der Aufruf von g in fib also auf die Funktion g in fib, nicht irgendein anderes g.
Hier eine Definition einer Potenzfunktion mit Hilfe einer verschachtelten Funktion, in der das Zwischenresultat als Parameter übergeben wird:
(define (hoch x n)
(define (h x n z)
(if (= n 0)
z
(h x (- n 1) (* x z))))
(h x n 1))
(define (hoch x n)
(define (h n z)
(if (= n 0)
z
(h (- n 1) (* x z))))
(h n 1))
Das x in (* x z) bezieht sich jetzt auf das nächste
umgebende x, also das von hoch.
Die Invariante von h ist:
z*xn_h = xn_hoch
wobei n_h und n_hoch die Parameter n der entsprechenden Funktionen sind.
(define (f x)
(define (g x)
(h 1))
(define (h y)
x)
(g 2))
(f 3)
Hier ruft f zunächst g auf, und das dann h. h liefert de Inhalt von x
als Resultat, wobei x sowohl in f als auch in g vorkommt. Auf welches
x bezieht sich das x in h jetzt?
Tatsächlich bezieht sich das x in h auf das x von f, die statisch naechst-äussere Definition von x. Das nennt man statische Bindung.
Die andere Alternative wäre, dass sich das x in h auf das x von g bezieht, die dynamisch nächst-äussere Definition von x (also im Aufrufbaum f-g-h).
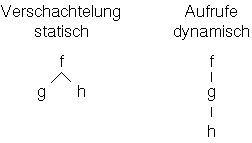
Die meisten Programmiersprachen verwenden die statische Bindung, um Namen von lokalen Variablen u.ä. aufzulösen. Der Grund dafür ist, dass man bei statischer Bindung nur die statischen Eigentschaften des Programms betrachten muss (hier die Verschachtelung), während man sich zur Auflösung von dynamischer Bindung die dynamischen Aufrufe überlegen muss, wobei verschiedene Aufrufe auf verschiedene dynamische Aufrufketten haben können.
Es gibt allerdings einige Elemente in vielen Programmiersprachen, bei denen es auf die dynamischen Aufrufe ankommt, z.B. Exceptions.
Die statische Bindung bedeutet, dass das früher gezeigte Modell der
Ausführung durch Erzeugung von let-Ausdrücken nicht stimmt. Fuer den
Aufruf (f 3) oben würde folgender Ausdruck herauskommen:
(let ((x 3)) (let ((x 2)) (let ((y 1)) x)))Dieser Ausdruck ergibt 2, und dieses Auswertungsmodell implementiert fälschlicherweise die dynamische Bindung. Man kann aber weiter mit diesem Modell arbeiten, wenn man zuerst die Namensbindungen durch Umbenennung eindeutig macht:
(define (f x-f)
(define (g x-g)
(h 1))
(define (h y-h)
x-f)
(g 2))
(f 3)
(let ((x-f 3)) (let ((x-g 2)) (let ((y-h 1)) x-f)))
(define (sumi n)
(if (= n 0)
1
(+ n (sumi (- n 1)))))
(define (sumqu n)
(if (= n 0)
1
(+ (qu n) (sumqu (- n 1)))))
Diese Definitionen sind einander ähnlich; Ähnlichkeiten in Programmen
sind ein Anzeichen, dass man die Gemeinsamkeiten in eine Definition
abstrahieren kann (auch oft faktorisieren genannt) und die
Unterschiede dann als Parameter übergeben kann. Das ist auch meistens
sinnvoll, z.B. damit man bei einer Erweiterung der Funktionalität der
Code nur an einer Stelle geändert werden muss.
Man kann dafuer sorgen, dass die Ähnlichkeiten noch größer werden, und das ist in vielen Fällen auch notwendig, wenn man die Gemeinsamkeiten herausarbeiten will:
(define (id x)
x)
(define (sumi n)
(if (= n 0)
0
(+ (id n) (sumi (- n 1)))))
(define (sumqu n)
(if (= n 0)
0
(+ (qu n) (sumqu (- n 1)))))
Jetzt ist der einzige Unterschied zwischen sumi und sumqu, welche
Funktion aufgerufen wird. Diese Funktion kann man jetzt als Parameter
übergeben:
(define (sum f n)
(if (= n 0)
0
(+ (f n) (sum f (- n 1)))))
(sum id 5)
(sum qu 5)
Wenn in einer Sprache mit einem bestimmten Datentyp alles gemacht
werden kann, was mit anderen Typen auch gemacht werden kann und Sinn
ergibt, spricht man von einem Datentyp erster Klasse. Funktionen sind
in Racket ein Typ erster Klasse, in vielen anderen Programmiersprachen
nicht.
(sum (lambda (x) x) 5)Dabei macht die Funktion
(lambda (x) x) das gleiche wie
die Funktion id oben.
Hier ein einfaches Beispiel einer unbenannten Funktion und ihrer Ausführung:
((lambda (x) (+ x 1)) 3) (let ((x 3)) (+ x 1)) (let ((x 3)) (+ 3 1)) (let ((x 3)) 4) 4Tatsächlich ist let nahe verwandt mit lambda. Man kann es einfach als Variante von Lambda sehen, bei der (im Gegensatz zu lambda) die formalen Parameter und die Argumente gleich nebeneinander stehen, was die Lesbarkeit erhöht; aber dafür kann man eine lambda-Funktion unabhängig von den Argumenten hinschreiben und auch verwenden (wie eben z.B. in Funktionen höherer Ordnung).
Hier ein Beispiel mit einem Aufruf:
(define (doppelt f x) (f (f x))) (doppelt (lambda (y) (* y 3)) 2) (let ((f (lambda (y) (* y 3))) (x 2)) (f (f x))) (let ((f (lambda (y) (* y 3))) (x 2)) (f ((lambda (y) (* y 3)) 2))) (let ((f (lambda (y) (* y 3))) (x 2)) (f (let ((y 2)) (* y 3)))) (let ((f (lambda (y) (* y 3))) (x 2)) (f 6)) (let ((f (lambda (y) (* y 3))) (x 2)) ((lambda (y) (* y 3)) 6)) (let ((f (lambda (y) (* y 3))) (x 2)) (let ((y 6)) (* y 3))) (let ((f (lambda (y) (* y 3))) (x 2)) (let ((y 6)) (* 6 3))) (let ((f (lambda (y) (* y 3))) (x 2)) (let ((y 6)) 18))
(define (hochn n)
(lambda (x)
(hoch x n)))
((hochn 4) 3)
(sum (hochn 3) 5)
(sum (let ((n 3)) (lambda (x) (hoch x n))) 5)
(sum (let ((n 3)) (lambda (x) (hoch x 3))) 5)
(sum (lambda (x) (hoch x 3)) 5)
(sum (lambda (x) (hoch x 3)) 5)
(let ((f (lambda (x) (hoch x 3))) (n 5)) (if (= n 1) 1 (+ (f n) (sum f (- n 1)))))
...
Die Übergabe der Parameter in zwei Stufen wie bei ((hochn 3)
4) statt gleichzeitig ((hoch 4 3)) bezeichnet man
als Currying, nach
dem mathematischen
Logiker Haskell
Brooks Curry (nach dem auch die Programmiersprachen Haskell und
Curry benannt sind).
Die Rückgabe von Funktionen erlaubt es, aus Funktionen neue Funktionen zu bauen, die dann anzuwenden, oder wieder zur Erzeugung einer weiteren Funktion zu benutzen:
(define (curry2 f)
(lambda (x)
(lambda (y)
(f x y))))
(((curry2 -) 2) 3)
(sum ((curry2 hoch) 3) 5)
(define (rcurry2 f)
(lambda (x)
(lambda (y)
(f y x))))
(((rcurry2 -) 2) 3)
(sum ((rcurry2 hoch) 3) 5)
(define (swap f)
(lambda (x y) (f y x)))
(sum ((curry2 (swap hoch)) 3) 5)
(define (cswap f)
(lambda (x) (lambda (y) ((f y) x))))
(sum ((cswap (curry2 hoch)) 3) 5)
Man kann damit auch Funktionen in einer Form definieren, die von
Parametern abstrahiert:
(define hochn (curry2 (swap hoch))) ((hochn 4) 3)Wenn man das weiterführt, kommt man zur Kombinatorischen Logik in der Mathematischen Logik. Und zwar lässt sich aus folgenden zwei Kombinatoren im Prinzip jede beliebige berechenbare Funktion bauen:
(define (K x)
(lambda (y) x))
(define (S x)
(lambda (y)
(lambda (z) ((x z) (y z)))))
Z.B. lässt sich die Funktion id oben, in der Kombinatorischen Logik I
genannt, wie folgt definieren:
(define I ((S K) K)) (I 15)Allerdings ist dieses Ergebnis eher für die Mathematik und theoretischen Informatik interessant als für die Programmierung.
Numerische Integration berechnet eine Näherung des Integrals einer Funktion in einem konkreten Intervall.
Eine einfache Variante davon ist es, den Wert der Funktion an n Stellen zu berechnen, und anzunehmen, dass die Funktion in der Nähe dieser Stellen jeweils den selben Wert ergibt. Damit kommt man zu der Formel
integral(f,a,b) = (f(a+dx/2)+f(a+dx+dx/2)+...+f(a+(n-1)*dx+dx/2))*dx
wobei die Schrittweite dx=(b-a)/n.
Statt dem Integral der Funktion f (rot) berechnet man das Integral
einer stufigen Annäherung an f (blau):
Tests:
(integral (lambda (x) 1) 0 1 50) (integral (lambda (x) x) 0 1 50) (integral (lambda (x) (* x x)) 0 1 50) (integral (lambda (x) (/ 1.0 x)) 1 2 1000) (integral (lambda (x) (/ 1.0 x)) 1 2.718 1000)Der erste Absatz beschreibt die Anforderungen (requirements) unseres Programms, darauf folgt eine Spezifikation, dann der Code, und die Tests.
Die bisherigen Versionen von hoch benoetigen n Aufrufe. Eine effizientere Implementierung basiert auf den Äquivalenzen
xn = (x2)n/2 wenn n gerade ist
xn = x*xn-1 wenn n ungerade ist
Wir können diese Version bauen, indem wir mit der ganz einfachen anfangen:
(define (hoch x n)
(if (= n 0)
1
(* x (hoch x (- n 1)))))
und dann noch einen weiteren Fall einfügen:
(define (hoch x n)
(if (= n 0)
1
(if (= (remainder n 2) 0)
(hoch (* x x) (/ n 2))
(* x (hoch x (- n 1))))))
Während der Aufruf (hoch x 34) bei der alten Funktion 34 weitere
Aufrufe benötigt, sind es bei dieser Funktion nur 7:

Besonders auffällig wird der Unterschied bei grossen n:
(hoch 1.0000001 10000000) (define a (hoch 2 200000))
Auf diese Weise kann man auch die Multiplikation aus der Addition aufbauen:
(define (mul x n)
(if (= n 0)
0
(if (= (remainder n 2) 0)
(mul (+ x x) (/ n 2))
(+ x (mul x (- n 1))))))
Diese Methode wird auf Prozessoren angewandt, die keinen
Multiplikationsbefehl eingebaut haben.
Jetzt kann man die Gemeinsamkeiten wieder in eine Funktion herausfaktorisieren und hoch und mul damit definieren.
Wie kann man hoch noch definieren? Eine Variante wäre:
xn = (x2)n/2 wenn n gerade ist
xn = x*(x2)(n-1)/2 wenn n ungerade ist
mit entsprechenden Abbruchbedingungen. Damit würde im Fall eines ungeraden n zwei Aufrufe zu einem zusammengefasst.
(define (hoch x n)
(if (= (remainder n 2) 0)
(if (= n 0)
1
(hoch (* x x) (/ n 2)))
(* x (hoch (* x x) (/ (- n 1) 2)))))
Diese Methode spart bei (hoch 2 34) einen Aufruf ein, wenn der ungerade Fall öfters vorkommt, entsprechend mehr:

Eine weitere Möglichkeit auf der Basis von:
xn = xfloor(n/2)*xceiling(n/2)
Dabei muss man auch n=1 als Abbruchbedingung verwenden, da ceiling(1/2)=1 ist:
(define (hoch x n)
(if (= n 0)
1
(if (= n 1)
x
(* (hoch x (floor (/ n 2)))
(hoch x (ceiling (/ n 2)))))))
Der Nachteil bei dieser Methode ist für diese Anwendung, dass es eine
doppelte Rekursion ist, sodass wir letztendlich wieder sogar mehr
Aufrufe haben wie bei der ursprünglichen Variante von hoch:
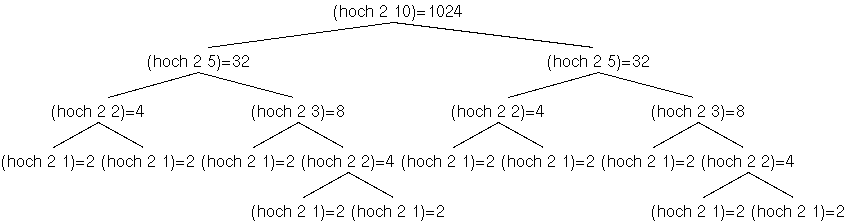
Wenn der Aufwand der Multiplikation allerdings von der Größe der multiplizierten Werte abhängt, was bei großen ganzen Zahlen in Racket der Fall ist, ist diese Methode aber immer noch schneller als die ursprüngliche, wie man beim Aufruf (hoch 2 200000) sieht.
Aus diesem Grund ist dieser Ansatz in anderen Bereichen, in denen die beiden Teile normalerweise nicht gleich sind, sehr sinnvoll und wird verwendet. Wenn man ihn zum Beispiel beim Sortieren einer Menge von Werten einsetzt, erhält man das Sortierverfahren mergesort.
Eine kleine Verbesserung dieser Variante ergibt sich aus der Beobachtung, dass bei n>=1 nie ein rekursiver Aufruf mit n=0 vorkommt. Daher muss man diesen Fall nur im nach aussen sichtbaren Aufruf abfangen:
(define (hoch x n)
(define (h x n)
(if (= n 1)
x
(* (h x (floor (/ n 2)))
(h x (ceiling (/ n 2))))))
(if (= n 0)
1
(h x n)))
Dadurch haben wir zwar in den meisten Fällen einen Aufruf mehr, aber
pro Aufruf muss weniger gemacht werden.